Rumus Luas Lingkaran: Cara Menghitung dan Penjelasan Lengkap

Lingkaran merupakan geometri yang sering ada dalam berbagai perhitungan matematika. Dalam konteks ini, rumus luas lingkaran merupakan dasar rumus yang harus diketahui oleh semua pelajar dan siapa pun yang tertarik dengan ilmu matematika. Perhitungan luas lingkaran sangat esensial dalam aplikasinya. Mulai dari desain hingga pengetahuan.

Artikel ini akan membahas secara lengkap tentang rumus luas lingkaran, cara menghitungnya, serta beberapa contoh soal yang dapat membantu memperjelas penerapan rumus tersebut. Mari kita simak lebih lanjut!

Baca juga Mengenai Apa Itu Adobe Firefly: AI Generatif yang Mengubah Dunia Kreatif

Rumus Luas Lingkaran

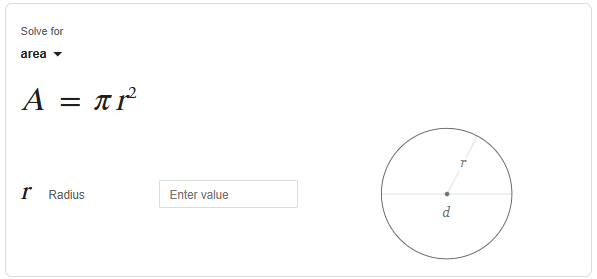
Luas lingkaran dapat dihitung dengan menggunakan rumus yang sangat sederhana, yaitu:

L=π×r2

Di mana:

• LLL adalah luas lingkaran,
• π\piπ adalah konstanta yang kira-kira bernilai 3.14 (atau 22/7),
• rrr adalah jari-jari lingkaran.

Jadi, untuk mencari luas lingkaran, Anda hanya perlu mengalikan nilai π\piπ dengan kuadrat dari jari-jari lingkaran.

Contoh Penerapan Rumus Luas Lingkaran:

Misalnya, kita memiliki sebuah lingkaran dengan jari-jari 7 cm. Maka, untuk menghitung luasnya:

L=3.14×72=3.14×49=153.86cm2

Sehingga, luas lingkaran tersebut adalah 153.86 cm².

Rumus Luas Setengah Lingkaran

Setengah lingkaran, atau sering disebut juga sebagai hemisphere, memiliki rumus luas yang sedikit berbeda. Jika kita tahu rumus luas lingkaran penuh, maka untuk mencari luas setengah lingkaran hanya cukup membagi hasil dari rumus luas lingkaran dengan dua.

Rumus untuk luas setengah lingkaran adalah:

Lsetengah​=1/2×π×r2

Contoh:

Misalnya kita memiliki setengah lingkaran dengan jari-jari 10 cm. Maka luasnya adalah:

Lsetengah​=1/2​×3.14×102=21​×3.14×100=157cm2

Jadi, luas setengah lingkaran tersebut adalah 157 cm².

Rumus Luas Seperempat Lingkaran

Rumus untuk luas seperempat lingkaran adalah konsep yang sangat mirip dengan rumus luas setengah lingkaran, hanya saja kali ini kita membagi hasilnya dengan empat, bukan dua. Jadi, rumus luas seperempat lingkaran adalah:

Lseperempat​=1/4​×π×r2

Contoh:

Jika kita memiliki seperempat lingkaran dengan jari-jari 8 cm, maka luasnya dapat dihitung sebagai berikut:

Lseperempat​=1/4​×3.14×82=1/4​×3.14×64=50.24cm2

Jadi, luas seperempat lingkaran tersebut adalah 50.24 cm².

Rumus Keliling Lingkaran

Selain menghitung luas, kita juga sering perlu menghitung keliling lingkaran. Keliling lingkaran adalah panjang garis yang mengelilingi lingkaran tersebut. Rumus keliling lingkaran adalah:

K=2×π×r

Di mana:

• KKK adalah keliling lingkaran,
• π\piπ adalah konstanta yang kira-kira bernilai 3.14,
• rrr adalah jari-jari lingkaran.

Contoh Penerapan Rumus Keliling Lingkaran:

Jika kita memiliki lingkaran dengan jari-jari 5 cm, maka keliling lingkaran tersebut adalah:

K=2×3.14×5=31.4cm

Sehingga, keliling lingkaran tersebut adalah 31.4 cm.

Unsur dan Bagian Lingkaran

Sebelum melangkah lebih jauh dalam menghitung luas dan keliling lingkaran, penting untuk memahami beberapa unsur dan bagian-bagian lingkaran yang ada. Berikut adalah penjelasan tentang bagian-bagian yang ada dalam lingkaran:

1. Jari-jari (r): Jari-jari adalah jarak dari pusat lingkaran ke sembarang titik pada keliling lingkaran. Ini adalah salah satu informasi yang paling penting dalam menghitung luas dan keliling lingkaran.
2. Diameter (d): Diameter adalah dua kali panjang jari-jari. Dengan kata lain, diameter adalah garis lurus yang melalui pusat lingkaran dan menghubungkan dua titik pada keliling lingkaran.
3. Pusat (O): Pusat lingkaran adalah titik di dalam lingkaran yang jaraknya sama dari semua titik di sepanjang keliling lingkaran.
4. Keliling (K): Keliling adalah panjang garis yang membentuk batas lingkaran.
5. Luas (L): Luas adalah ukuran dari ruang yang terdapat di dalam lingkaran.

Contoh Soal Menghitung Rumus Lingkaran

Untuk membantu pemahaman, berikut adalah beberapa contoh soal menghitung rumus lingkaran beserta langkah-langkah perhitungannya.

Contoh Soal 1: Menghitung Luas Lingkaran

Diketahui sebuah lingkaran dengan jari-jari 14 cm. Hitunglah luas lingkaran tersebut!

Penyelesaian:

L=π×r2=3.14×142=3.14×196=615.44cm2

Jadi, luas lingkaran tersebut adalah 615.44 cm².

Contoh Soal 2: Menghitung Keliling Lingkaran

Diketahui sebuah lingkaran dengan diameter 20 cm. Hitunglah keliling lingkaran tersebut!

Penyelesaian:

Karena diameter lingkaran diberikan, kita perlu mencari jari-jari terlebih dahulu. Jari-jari adalah setengah dari diameter.

r=d/2​=20/2=10cm

Sekarang, kita dapat menghitung keliling lingkaran:

K=2×π×r=2×3.14×10=62.8cm

Jadi, keliling lingkaran tersebut adalah 62.8 cm.

Contoh Soal 3: Menghitung Luas Setengah Lingkaran

Jika sebuah lingkaran memiliki jari-jari 8 cm, berapa luas setengah lingkarannya?

Penyelesaian:

Gunakan rumus luas setengah lingkaran:

Lsetengah​=1/2​×π×r2=1/2​×3.14×82=1/2×3.14×64=100.48cm2

Jadi, luas setengah lingkaran tersebut adalah 100.48 cm².

Cara Menghitung Luas Lingkaran dengan Tepat

Menghitung luas lingkaran mungkin terdengar sederhana, tetapi penting untuk memperhatikan beberapa hal agar perhitungan Anda benar. Berikut adalah langkah-langkah untuk menghitung luas lingkaran dengan tepat:

1. Ketahui Jari-jari Lingkaran: Langkah pertama adalah mengetahui panjang jari-jari lingkaran. Jika yang diberikan adalah diameter, pastikan untuk membaginya dua kali.
2. Gunakan Nilai π\piπ yang Tepat: Anda bisa menggunakan nilai π\piπ yang lebih akurat, seperti 3.14159, atau cukup menggunakan 3.14 untuk kemudahan.
3. Terapkan Rumus Luas Lingkaran: Setelah mengetahui jari-jari dan nilai π\piπ, terapkan rumus L=π×r2untuk menghitung luas lingkaran.
4. Selesaikan Perhitungan: Lakukan perhitungan matematika sesuai dengan rumus dan hasilkan nilai luas lingkaran.

Untuk mengakses konten terkait yang lebih banyak, silahkan untuk mengunjungi website Utama kami.

Kesimpulan

Dalam artikel ini, kita telah mempelajari rumus luas lingkaran, bagaimana cara menghitungnya, serta contoh soal yang bisa membantu memperjelas penerapan rumus tersebut. Lingkaran adalah salah satu bentuk geometri yang sangat penting, baik dalam matematika dasar maupun aplikasi praktis di kehidupan sehari-hari. Dengan memahami cara menghitung luas dan keliling lingkaran, Anda dapat lebih percaya diri dalam mengerjakan soal-soal geometri atau menerapkannya dalam situasi nyata.

Referensi:

• Stewart, J. (2016). Calculus: Early Transcendentals. Cengage Learning.
• Larson, R., & Edwards, B. H. (2017). Calculus of a Single Variable. Brooks/Cole.
• Hille, E. (2019). Mathematical Methods in the Physical Sciences. Wiley.

Penulis Eko Bahran Adinata Direktorat Puti